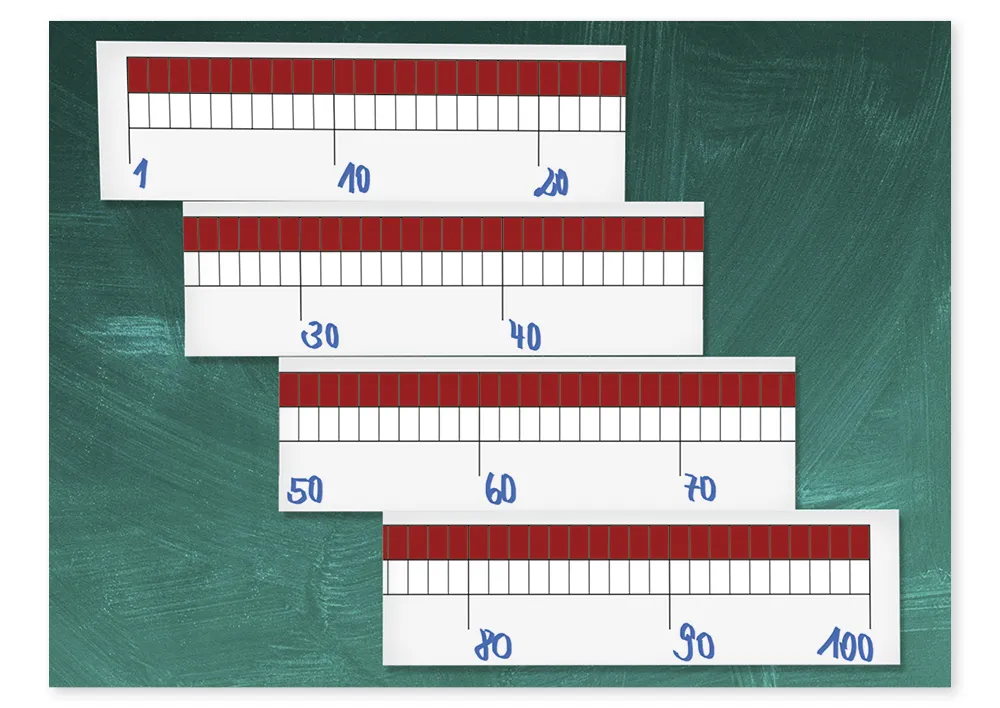
De getallenlijn dient één doel: het stelt abstracte getallenruimten en getallen voor op een rechte lijn. De relatie tussen getallen wordt zo verduidelijkt. Een getallenlijn biedt oriëntatie in grote getallenruimten die niet meer zonder hulpmiddelen geteld kunnen worden. De getallenlijn maakt het gemakkelijker om optel- en aftrekopgaven te begrijpen. Kinderen kunnen gemakkelijk rekenen oefenen en consolideren zonder te tellen! Lees meer...
-
 Lesmateriaal - hulpmiddelen
Lesmateriaal - hulpmiddelen
-
 Kantoorbenodigdheden
Kantoorbenodigdheden
-
 Kleuter- en onderbouwmateriaal
Kleuter- en onderbouwmateriaal
- Voorbereidend en beginnend rekenen
- IT & digitaal
- Natuur & onderzoeken
- Techniek & bouwen
- Spelend leren
- Muziek
- Creatief & expressie
- Kantoorbenodigdheden
- Cadeaus
- NIEUW
- SALE
-
 Leermiddelen groep 3-8
Leermiddelen groep 3-8
- Rekenen
- Taal
- Engels / Frans
- Zaakvakken
- Educatieve dobbelstenen
- Bewegend leren
- Digitaal leren
- fischertechnik education GS
- Digitaal leren
- Educatieve spellen
- Montessori materiaal
- Muziek
- Taalontwikkeling
-
 Voortgezet Onderwijs
Voortgezet Onderwijs
-
 De Jonge Onderzoeker
De Jonge Onderzoeker
-
 Creatief + knutselen
Creatief + knutselen
-
 Opbergen - meubilair
Opbergen - meubilair
- Nieuw
- Sale
Basiskennis wiskunde: De getallenlijn
De getallenlijn dient één doel: het stelt abstracte getallenruimten en getallen voor op een rechte lijn. De relatie tussen getallen wordt zo verduidelijkt. Een getallenlijn biedt oriëntatie in grote getallenruimten die niet meer zonder hulpmiddelen geteld kunnen worden. De getallenlijn maakt het gemakkelijker om optel- en aftrekopgaven te begrijpen. Kinderen kunnen gemakkelijk rekenen oefenen en consolideren zonder te tellen! Lees meer...
Wat is een getallenlijn?
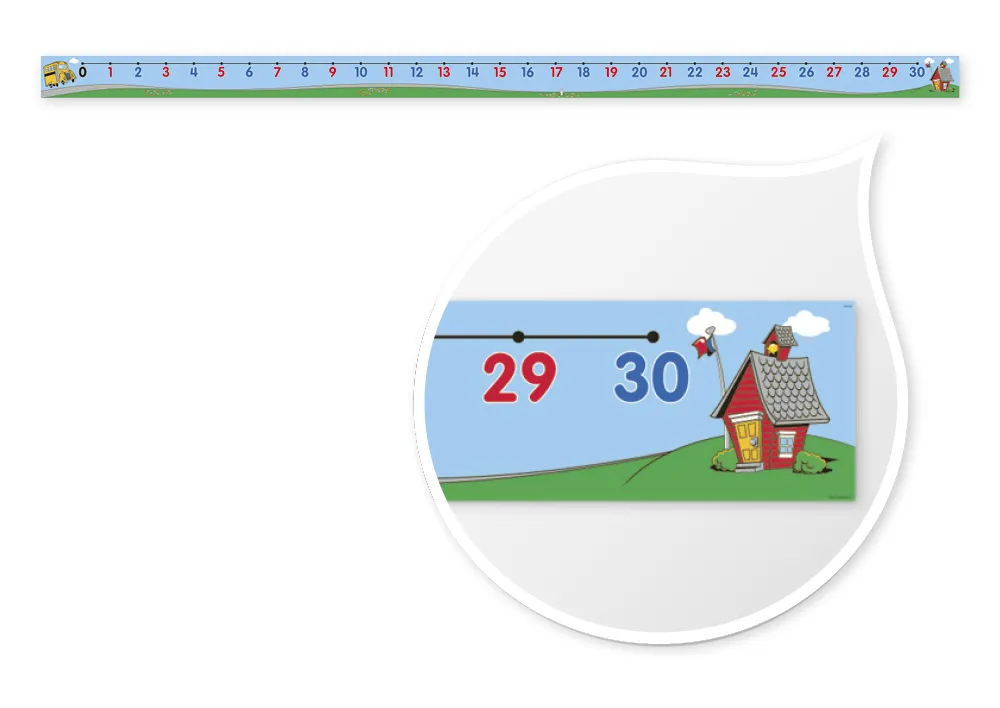
Een getallenlijn is een van de vele manieren om natuurlijke getallen voor te stellen. De getallenlijn is oneindig lang. Hij loopt altijd van links naar rechts. Dit betekent dat zelfs grote getallenruimtes gevisualiseerd kunnen worden. Een getallenlijn voor wiskunde maakt het makkelijker voor leerlingen om zich getallen voor te stellen en te visualiseren.
Op de basisschool wordt in eerste instantie alleen gekeken naar natuurlijke getallen. In de getallenlijnoefeningen is het beginpunt van de getallenlijn nul en eindigt bij 20, 100 of 1000, afhankelijk van het klasniveau. De getallenlijn wordt later uitgebreid met negatieve getallen.
Een getallenlijn tot 1000 is vooral nuttig in klas 3 en 4 van de basisschool om berekeningen en rekenstappen te visualiseren. Vanaf leerjaar 3 wordt de tientallenovergang beheerst. Daarna zijn er vaak alleen nog maar getallenlijnen verdeeld in stappen van tien.
In het vak wiskunde maakt de getallenlijn voor de basisschool het voor leerkrachten makkelijker om rekenfeiten uit te leggen. Oefeningen met de getallenlijn kunnen bijvoorbeeld worden gebruikt om te laten zien en te controleren welke van twee getallen de grootste is. Optel- en aftrekoefeningen kunnen ook gevisualiseerd worden op de getallenlijn voor wiskunde. De getallenlijn maakt abstracte opgaven met grote natuurlijke getallen dus makkelijker. De getallenlijn is ideaal voor verschillende oefeningen en opgaven met de overgang van tientallen, optellen en aftrekken naar vermenigvuldigen.
Rekenen met de getallenlijn op de basisschool
De getallenlijn op de basisschool is vooral geschikt om kinderen een overzicht te geven van verschillende getallenreeksen. De getallenlijn zorgt voor een goede oriëntatie binnen het getallengebied, ongeacht of dit de getallen tot 20, 100 of 1000 omvat.
Het is vooral belangrijk dat kinderen zich goed kunnen oriënteren als er een nieuw getallengebied wordt ontwikkeld, bijvoorbeeld als onderdeel van de tientallenovergang. Ze moeten bijvoorbeeld een gevoel ontwikkelen voor hoe groot de afstanden tussen de individuele getallen zijn en hoe de natuurlijke getallen zich tot elkaar verhouden. Je kunt de rekenvaardigheden van kinderen vooral ontwikkelen met getallenlijnoefeningen!
De eerste categorisering van getallen kan bijvoorbeeld worden uitgevoerd als onderdeel van eenvoudige zoekoefeningen. Leerlingen moeten zoeken naar gegeven getallen op de getallenlijn en ze markeren in kleur. De volgende stap is het aflezen van de afstanden tussen de getallen op de getallenlijn als eerste stap naar optellen en aftrekken. Deze zoekspelletjes zijn leuk voor de kinderen en maken ze enthousiast over de getallenlijn!
Getallenlijnoefeningen voor wiskunde op de basisschool
Oefeningen voor optellen en aftrekken kunnen worden gedaan op de getallenlijn met natuurlijke getallen. Bij getallenlijnoefeningen moeten de kinderen pijlen tekenen op de getallenlijn met behulp van een liniaal. De lengte van de pijlen moet overeenkomen met de individuele sommandes of, in het geval van aftrekken, de min- en subtrede. In het geval van optellen worden de pijlen gewoon samengevoegd. De kinderen kunnen dan het resultaat van de berekening aflezen bij het eindpunt van de resulterende totaalpijl.
Bij aftrekken wordt eerst een pijl naar rechts getrokken langs de getallenlijn, waarvan de lengte overeenkomt met de minuend. De subtrede, d.w.z. het getal dat moet worden afgetrokken, wordt weergegeven als een pijl die begint bij het eindpunt van de eerste lijn. Deze pijl moet naar links wijzen.
De berekening wordt extra duidelijk als de kinderen de afzonderlijke pijlen in verschillende kleuren tekenen. Voor nog meer duidelijkheid wordt het resultaat in dezelfde kleur gemarkeerd. Dit maakt de oefening op de getallenlijn op de basisschool ook veel spannender en afwisselender voor veel kinderen.
Later kan de rekengetallenlijn ook gebruikt worden om langzaam vermenigvuldigingsopgaven te introduceren. Bijvoorbeeld met de oefening "Rekenen met stappen van 8". In deze getallenreeksoefeningen wordt een soort kettingtelling gebruikt. Hierbij wordt dezelfde waarde steeds opnieuw opgeteld. De leerlingen kunnen gewoon het corresponderende aantal punten op de getallenlijn tellen. Daarna tekenen ze bijvoorbeeld een gebogen pijl naar het corresponderende punt. Deze oefening heeft zijn equivalent in tafels van vermenigvuldiging.
Zoals je kunt zien, kan de getallenlijn op de basisschool worden gebruikt om nog complexere feiten op een begrijpelijke manier te visualiseren en uit te leggen!