Ringbord, compact, complete set

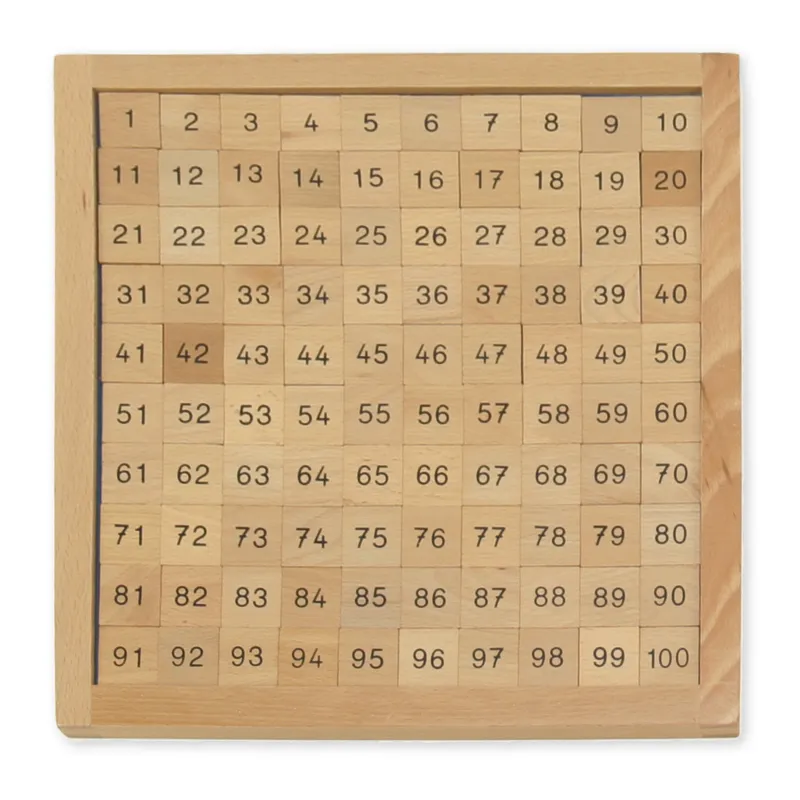
Dit exclusieve en veelzijdige ringbord is geschikt voor gebruik in de basisschool en het voortgezet onderwijs. Het bestaat uit een houten werkbord bedrukt met de cijfers 1 - 100 en 100 ringvormige gefreesde gaatjes. De bijpassende houten kist en houten ringen zijn gelakt in de 10 Montessori kleuren. De zwarte ringen staan voor priemgetallen. Door de heel nauwkeurig gefreesde inkepingen kunnen de houten ringen gericht worden geplaatst en gestapeld. De op het houten werkbord gedrukte cijfers blijven zichtbaar tijdens het werken dankzij het gebruik van ringen in plaats van fiches. Met dit ringbord kan dus aan de slag gegaan worden met de complexe bewerkingen binnen het getallengebied tot 100 en houdt rekening met de volgende aspecten: Opbouw van de getallen tot 100, de tafels t/m 10 met de kleurrijen tot 100, uitwerken van de priemgetallen (de zgn. Zeef van Eratosthenes), kleinste gemene veelvoud en grootste gemene deler.

Leermogelijkheden
Het verkennen van de veelvouden in het honderd veld

Mogelijke toepassingen
Basis- en voortgezet onderwijs

Methodisch - didactische suggesties
Het kind kiest een rij van de tafels van vermenigvuldiging (b.v. de tafel van drie), neemt roze ringen en plaatst ze op alle getallen die deelbaar zijn door 3. Als je aan een tweede rij werkt, zijn er al overlappingen. De priemgetallen blijven over.

Aanbieding & oefening
De kinderen ervaren het tellen en leren zich te oriënteren op de honderdveld. Welk getal waar is, voorganger of opvolger, het besef dat alle gelijke enen verticaal gerangschikt zijn en alle gelijke tientallen horizontaal. In deze leerfase kan ook gebruik worden gemaakt van de meegeleverde fiches. Bedek de getallen en vraag welk getal eronder verborgen is, of geef opdrachten om verschillende getallen te bedekken. Hier zijn talloze oefeningen mogelijk om het getallengebied te automatiseren.

Een andere manier om met het ringbord te werken is te werken aan de tafels van vermenigvuldiging. Aangezien in het begin gewoonlijk slechts tot 10 x ... wordt gewerkt, wordt hier de ringstandaard gebruikt. Op de standaard staan 10 ringen per kleur (behalve zwart) in oplopende kleur = cijferreeks van 1 - 10. De controle geschiedt door het eigen patroon, dat elke vermenigvuldigingsrij vertoont. Natuurlijk mogen de kinderen volgens het patroon leggen. Het doel hier is om de  tafels te automatiseren. Veel kinderen gaan al verder dan 10 x ... omdat het spannend is om te weten, bijvoorbeeld, hoeveel 15 x 3 is en dat je dit ook kunt berekenen.

De volgende stap is het leggen van "verwante" vermenigvuldigingsrijen, b.v. 3, 6 en 9. Hier wordt duidelijk waarom het bord een "ring bord" wordt genoemd en niet een vermenigvuldigbord. Omdat er nu ringen op elkaar worden geplaatst. Bijvoorbeeld, bij het leggen van de tafels van 3, 6 en 9 op het getal 18, zijn er drie ringen van verschillende kleuren. Uiterlijk op dit punt moeten de begrippen "deler" en "veelvoud" worden geïntroduceerd, omdat het bord duidelijk laat zien wat bij elkaar hoort.

Priemgetallen: Als het kind nu alle vermenigvuldigingsrijen tot 100 neerlegt, in de Montessori-kleuren, blijven sommige vierkanten leeg. Hierdoor worden de priemgetallen duidelijk zichtbaar. Nu is het ringbord ook een boeiend hulpmiddel voor oudere kinderen. Nu kan  gewerkt worden aan de deelbaarheidsregels en de priemgetallen in het getallengebied tot 100 met concreet materiaal, zonder papier en potlood. Ook hier vormt de reeds vertrouwde structuur van de kleurenserie een controle.

Priemfactorontbinding: Het interessantste detail van het ringbord is misschien wel dat het kan worden gebruikt om priemfactoren te ontbinden en zo de grootste gemene deler en de kleinste gemene veelvoud te bepalen. Met het ringbord kan dit gemakkelijk en duidelijk uitgewerkt worden. Het kind markeert bijvoorbeeld het getal 18 op het lege bord met een fiche om verwarring te voorkomen. Begin nu met het kleinst mogelijke priemgetal 2, zeg 18:2=9 en plaats de groene ring voor priemfactor 2 op 9. Nu is het kleinst mogelijke priemgetal 3. 9:3=3, een roze ring wordt op 3 geplaatst. Kleinst mogelijke priemgetal weer 3, 1 roze ring wordt op 1 geplaatst. Nu worden de ringen verzameld, gesorteerd en de bijbehorende getallen opgeschreven, in dit geval 1 groene en twee roze ringen, dus: 2x3x3=18, dus de priemfactoren zijn 2, 3, 3. Om de ggd en de kgv van twee of meer getallen te bepalen, hoeven de vastgestelde priemfactoren van de getallen dan alleen nog maar te worden gecombineerd en dienovereenkomstig te worden berekend.

Door deze veelzijdige gebruiksmogelijkheden van het ringbord is dit materiaal al geschikt als werk- en oefenmateriaal voor kinderen vanaf de leeftijd van 3 jaar en begeleidt het de kinderen tot en met groep 8 en zelfs daarna. De ringen zijn robuust, liggen goed in de hand en mochten er ringen zoekraken, dan kunnen die natuurlijk altijd worden bijbesteld, een aantal extra reserveringen worden al meegeleverd.

Afmetingen: 45 x 45 x 7,5 cm, ring diameter 3 cm

• voor complexe bewerkingen met getallen t/m 100
• veelzijdige gebruiksmogelijkheden
• priemgetallen, kleinste gemene veelvoud en grootste gemene deler
• geschikt voor po & vo

Materiaal
Beukenhout

Milieu & veiligheid
Hout van duurzame teelt

! Dit materiaal is geen speelgoed, maar educatief materiaal. Bevat kleine onderdelen! Daarom alleen gebruiken onder toezicht van gekwalificeerde professionals !